facebook | mathema.romania@gmail.com
Memorator Algebră
clasele 5 - 8
✦ Graficul funcției \({h: \textcolor{#ed09e2}{D} \rightarrow \mathbf{R}}\), \({h(x) = ax + b}\), \({\textcolor{#ed09e2}{D}}\) interval nemărginit ❖ graficul este o semidreaptă
Domeniul de definiție e de forma \({(c, + \infty)}\) sau \({[c, + \infty)}\) sau \({(- \infty, c)}\) sau \({(- \infty, c]}\).
Varianta 1
- se desenează graficul funcției, extinzând domeniul de definiție la \({\mathbf{R}}\) și păstrând aceeași lege de corespondență
- mai exact, desenăm graficul funcției \({f: \textcolor{#ed09e2}{\mathbf{R}} \rightarrow \mathbf{R}}\), \({f(x) = ax + b}\)
- din acest grafic se păstrează porțiunea corespunzătoare mulțimii \({D}\)
- pe axa Ox reprezentăm capătul \({c}\) al intervalului de definiție
- proiectăm capătul \({c}\) al intervalului pe grafic
- păstrăm din grafic semidreapta determinată de proiecția lui c pe grafic
- marcăm capătul semidreptei cu semnul de interval deschis (paranteză rotundă) sau interval închis (paranteză dreaptă), după cum e precizat în domeniul de definiție al funcției
- exemplu: să desenăm graficul funcției \({h: \textcolor{#ed09e2}{(-1, + \infty)} \rightarrow \mathbf{R}}\), \({h(x) = 2x + 4}\);
- am desenat mai sus graficul funcției \({f: \textcolor{#ed09e2}{\mathbf{R}} \rightarrow \mathbf{R}}\), \({f(x) = 2x + 4}\), care are aceeași lege de corespondență ca și funcția \({h}\)
- pe axa Ox marcăm capătul intervalului \({(-1, + \infty)}\), adică pe -1
- proiectăm capătul intervalului pe graficul funcției \({f}\), adică prin -1 ducem dreapta perpendiculară pe axa Ox și marcăm punctul de intersecție al acestei drepte cu graficul funcției \({f}\)
- porțiunea care începe cu proiecția lui -1 pe grafic și se contiuă la \({ + \infty}\) este graficul funcției \({h}\) (semidreapta desenată cu albastru)
- marcăm capătul semidreptei cu semnul de interval deschis (paranteză rotundă) pentru că domeniul de definiție e deschis la -1
![Graficul funcției definite pe intervalul (-1, plus infinit], f(x) = 2x + 4](/imagini/memorator/graficul-functiei-2x-plus-4-definita-pe-intervalul-minus-1-plus-infinit-deschis-la-minus-1.png)
Varianta 2
- fie \({c}\) capătul intervalului de definiție
- calculăm \({h(c)}\); obținem punctul \({A(c, f(c))}\)
- alegem convenabil (pentru calcule ușoare) un element \({d}\) din domeniul de definiție
- calculăm \({h(d)}\); obținem punctul \({B(d, h(d))}\)
- în sistemul xOy desenăm punctele \({A(c, h(c))}\) și \({B(d, h(d))}\)
- desenăm semidreapta determinată de punctele \({A(c, h(c))}\) și \({B(d, h(d))}\), cu originea în punctul corespunzător capătului domeniului de definiție
- marcăm originea semidreptei cu semnul de interval deschis (paranteză rotundă) sau interval închis (paranteză dreaptă), după cum ne indică domeniul de definiție
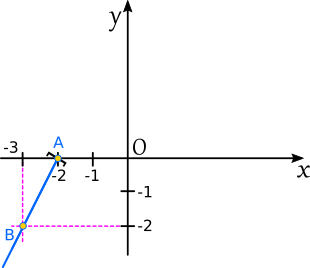
- exemplu: să desenăm graficul funcției \({h: \textcolor{#ed09e2}{(-\infty, -2]} \rightarrow \mathbf{R}}\), \({h(x) = 2x + 4}\);
- capătul intervalului de definiție este -2
- calculăm \({h(-2) = 2 \cdot (-2) + 4 = 0}\); obținem punctul \({A(-2, 0)}\)
- alegem convenabil un număr din intervalul \({(-\infty, -2]}\); alegem -3
- calculăm \({h(-3) = 2 \cdot (-3) + 4 = -2}\); obținem punctul \({B(-3, -2)}\)
- reprezentăm punctele \({A(-2, 0)}\) și \({B(-3, -2)}\) în sistemul de axa xOy
- desenăm semidreapta determinată de punctele \({A(-2, 0)}\) și \({B(-3, -2)}\), cu originea în \({A(-2, 0)}\)
- marcăm capătul din dreapta al segmentului cu semnul „]” corespunzător intervalului închis, pentru că domeniul de definiție e închis la -2