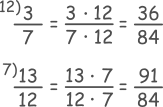facebook | mathema.romania@gmail.com
Memorator Algebră
clasele 5 - 8
- Numere naturale
- Ce sunt numerele naturale
- Scrierea și citirea numerelor naturale
- Scrierea unui număr natural ca sumă de produse
- Succesor. Predecesor
- Aproximarea. Estimarea. Rotunjirea
- Reprezentarea pe axa numerelor
- Compararea numerelor naturale
- Operații cu numere naturale
- • Adunarea
- • Scăderea
- • Înmulțirea. Factor comun
- • Împărțirea
- Ordinea operațiilor +, -, x, :
- Puterea cu exponent natural a unui număr natural
- Divizibilitatea
- Descompunerea unui număr natural în produs de puteri de numere prime
- Cel mai mare divizor comun (c.m.m.d.c.)
- Cel mai mic multiplu comun (c.m.m.m.c.)
- Proprietăţile divizibilităţii numerelor naturale
- Ce sunt fracţiile
- Fracţii subunitare, echiunitare, supraunitare
- Fracţii echivalente
- Reprezentarea fracţiilor pe axa numerelor
- Compararea fracţiilor
- Introducerea întregilor în fracţie
- Scoaterea întregilor din fracţie
- Amplificarea fracţiilor
- Simplificarea fracţiilor
- Fracţii ireductibile
- Aducerea fracţiilor la acelaşi numitor
- Adunarea şi scăderea fracţiilor
- Înmulţirea fracţiilor
- Împărţirea fracţiilor
- O fracţie dintr-un număr. O fracţie dintr-o fracţie
- Procente. Procent dintr-un număr. Procent dintr-o fracţie
- Media aritmetică
- Puterea unei fracţii
- Ce este fracţia zecimală
- Transformarea unei fracţii ordinare în fracţie zecimală
- Transformarea unei fracţii zecimale în fracţie ordinară
- Reprezentarea fracţiilor zecimale pe axa numerelor
- Compararea fracţiilor zecimale
- Adunarea şi scăderea fracţiilor zecimale
- Înmulțirea fracțiilor zecimale cu un număr finit de zecimale nenule
- Împărțirea a două numere naturale cu rezultat fracție zecimală
- Împărţirea unei fracţii zecimale cu un număr finit de zecimale nenule la un număr natural nenul
- Ce sunt numerele întregi
- Adunarea numerelor întregi
- Scăderea numerelor întregi
- Înmulţirea numerelor întregi
- Împărţirea numerelor întregi
- Puterea cu exponent număr natural a unui număr întreg nenul
- Ordinea efectuării operaţiilor şi folosirea parantezelor - numere întregi
- Ecuaţii care se rezolvă în mulţimea numerelor întregi
- Probleme care se rezolvă cu ajutorul ecuaţiilor în \({ℤ}\)
- Inecuaţii care se rezolvă în mulţimea numerelor întregi
- Probleme care se rezolvă cu ajutorul inecuaţiilor în \({ℤ}\)
- Ce sunt numerele raţionale
- • Relaţia între numerele naturale, numerele întregi şi numerele raţionale
- • Opusul unui număr rațional
- • Reprezentarea pe axă a unui număr rațional
- • Modulul unui număr rațional
- • Compararea numerelor raționale
- Adunarea și scăderea numerelor raţionale
- • Proprietăți
- Înmulţirea numerelor raţionale
- Împărţirea numerelor raţionale
- Puterea cu exponent număr întreg a unui număr raţional nenul
- Ordinea efectuării operaţiilor cu numere raţionale şi folosirea parantezelor
- Ecuaţii de gradul 1 în mulţimea numerelor raţionale
- Probleme care se rezolvă cu ajutorul ecuaţiilor în mulţimea numerelor raţionale
- Rădăcina pătrată a pătratului unui număr natural
- Rădăcina pătrată a pătratului unui număr întreg
- Rădăcina pătrată a pătratului unui număr rațional
- Cum încadrăm un număr între două pătrate perfecte consecutive
- Aproximarea rădăcinii pătrate a unui număr rațional pozitiv
- Scoaterea factorilor de sub radical
- Introducerea factorilor sub radical
- Numere iraționale
- Mulțimea numerelor reale
- Modulul unui număr real
- Compararea și ordonarea numerelor reale
- Reprezentarea prin aproximări a numerelor reale pe axa numerelor
- Operații cu numere reale
- • Adunarea și scăderea
- • Înmulțirea
- • Împărțirea
- • Puteri cu exponent număr întreg
- • Reguli de calcul cu radicali
- • Ordinea efectuării operațiilor
- Raționalizarea numitorului (prima parte) de forma \({a\sqrt{b}}\)
- Media geometrică (proporțională) a două numere reale pozitive
- Media aritmetică ponderată
- Ecuații de forma \({x^2 = a \in \mathbf{R}}\)
sisteme de ecuaţii liniare
- Transformarea unei egalități într-o egalitate echivalentă. Identități
- Ecuații de forma \({ax + b = 0 }\), \({a, b \in \mathbf{R}}\)
- Sisteme de două ecuații liniare cu două necunoscute
- • Metoda substituției
- • Metoda reducerii
- Probleme care se rezolvă cu ajutorul ecuațiilor
- Probleme care se rezolvă cu ajutorul sistemelor de ecuații
- Expresii algebrice
- Operații cu numere reale reprezentate prin litere
- • Adunarea și scăderea
- • Înmulțirea, împărțirea, ridicarea la putere
- Formule de calcul prescurtat
- • Raționalizarea numitorului - partea a doua
- Descompuneri în factori
- Fracții algebrice
- • Ce sunt fracțiile algebrice
- • Amplificarea și simplificarea fracțiilor algebrice
- • Operații cu fracții algebrice
- • Adunarea și scăderea fracțiilor algebrice
- • Înmulțirea fracțiilor algebrice
- • Împărțirea fracțiilor algebrice
- • Ridicarea la putere a fracțiilor algebrice
a datelor
- Organizarea datelor. Tabele. Frecvențe
- Grafice
- • Grafice cu bare verticale (coloane)
- • Grafice cu bare orizontale (benzi)
- • Grafice cu linii
- • Diagrame circulare
- Indicatorii tendinței centrale
- • Media
- • Mediana
- • Modul și amplitudinea
- Probabilități
- Produs cartezian
- Sistem de axe ortogonale
- Distanța dintre două puncte știind coordonatele lor. Mijlocul unui segment
- 1. Numere naturale
- • Ce sunt numerele naturale
- • Scrierea și citirea numerelor naturale
- • Scrierea unui număr natural ca sumă de produse
- • Succesor. Predecesor
- • Aproximarea. Estimarea. Rotunjirea
- • Reprezentarea pe axa numerelor
- • Compararea numerelor naturale
- • Operații cu numere naturale
- • Adunarea
- • Scăderea
- • Înmulțirea. Factor comun
- • Împărțirea
- • Ordinea operațiilor +, -, x, :
- 2. Puterea cu exponent natural a unui număr natural
- • Ce sunt puterile. Pătratul unui număr natural
- • Reguli de calcul cu puteri
- • Compararea puterilor
- • Scrierea în baza 10. Scrierea în baza 2
- • Ordinea operațiilor +, -, x, :, ab
- 3. Divizibilitatea
- • Divizor. Multiplu
- • Criterii de divizibilitate
- • Numere prime. Numere compuse
- • Ciurul lui Eratostene
- • Cum stabilim dacă un număr natural este prim
- • Descompunerea unui număr natural în produs de puteri de numere prime
- • Cel mai mare divizor comun (c.m.m.d.c.)
- • Cel mai mic multiplu comun (c.m.m.m.c.)
- • Proprietăţile divizibilităţii numerelor naturale
- 4. Fracţii
- • Ce sunt fracţiile
- • Fracţii subunitare, echiunitare, supraunitare
- • Fracţii echivalente
- • Reprezentarea fracţiilor pe axa numerelor
- • Compararea fracţiilor
- • Introducerea întregilor în fracţie
- • Scoaterea întregilor din fracţie
- • Amplificarea fracţiilor
- • Simplificarea fracţiilor
- • Fracţii ireductibile
- • Aducerea fracţiilor la acelaşi numitor
- • Adunarea şi scăderea fracţiilor
- • Înmulţirea fracţiilor
- • Împărţirea fracţiilor
- • O fracţie dintr-un număr. O fracţie dintr-o fracţie
- • Procente. Procent dintr-un număr. Procent dintr-o fracţie
- • Media aritmetică
- • Puterea unei fracţii
- 5. Fracții zecimale
- • Ce este fracţia zecimală
- • Transformarea unei fracţii ordinare în fracţie zecimală
- • Transformarea unei fracţii zecimale în fracţie ordinară
- • Reprezentarea fracţiilor zecimale pe axa numerelor
- • Compararea fracţiilor zecimale
- • Adunarea şi scăderea fracţiilor zecimale
- • Înmulțirea fracțiilor zecimale cu un număr finit de zecimale nenule
- • Împărțirea a două numere naturale cu rezultat fracție zecimală
- • Împărţirea unei fracţii zecimale cu un număr finit de zecimale nenule la un număr natural nenul
- 6. Mulțimi
- • Ce sunt mulţimile
- • Relaţii între mulţimi
- • Operaţii cu mulţimi
- • Mulțimi speciale
- 7. Rapoarte şi proporţii
- • Ce sunt rapoartele şi proporţiile
Proprietatea fundamentală a proporţiilor - • Determinarea unui termen necunoscut dintr-o proporție
- • Proporții derivate
- • Șir de rapoarte egale
- • Mărimi direct proporționale
- • Mărimi invers proporționale
- • Regula de trei simplă
- 8. Numere întregi
- • Ce sunt numerele întregi
- • Adunarea numerelor întregi
- • Scăderea numerelor întregi
- • Înmulţirea numerelor întregi
- • Împărţirea numerelor întregi
- • Puterea cu exponent număr natural a unui număr întreg nenul
- • Ordinea efectuării operaţiilor şi folosirea parantezelor - numere întregi
- • Ecuaţii care se rezolvă în mulţimea numerelor întregi
- • Probleme care se rezolvă cu ajutorul ecuaţiilor în \({ℤ}\)
- • Inecuaţii care se rezolvă în mulţimea numerelor întregi
- • Probleme care se rezolvă cu ajutorul inecuaţiilor în \({ℤ}\)
- 9. Numere raţionale
- • Ce sunt numerele raţionale
- • Relaţia între numerele naturale, numerele întregi şi numerele raţionale
- • Opusul unui număr rațional
- • Reprezentarea pe axă a unui număr rațional
- • Modulul unui număr rațional
- • Compararea numerelor raționale
- • Adunarea și scăderea numerelor raţionale
- • Proprietăți
- • Înmulţirea numerelor raţionale
- • Împărţirea numerelor raţionale
- • Puterea cu exponent număr întreg a unui număr raţional nenul
- • Ordinea efectuării operaţiilor cu numere raţionale şi folosirea parantezelor
- • Ecuaţii de gradul 1 în mulţimea numerelor raţionale
- • Probleme care se rezolvă cu ajutorul ecuaţiilor în mulţimea numerelor raţionale
- 10. Numere reale
- • Rădăcina pătrată a pătratului unui număr natural
- • Rădăcina pătrată a pătratului unui număr întreg
- • Rădăcina pătrată a pătratului unui număr rațional
- • Cum încadrăm un număr între două pătrate perfecte consecutive
- • Aproximarea rădăcinii pătrate a unui număr rațional pozitiv
- • Scoaterea factorilor de sub radical
- • Introducerea factorilor sub radical
- • Numere iraționale
- • Mulțimea numerelor reale
- • Modulul unui număr real
- • Compararea și ordonarea numerelor reale
- • Reprezentarea prin aproximări a numerelor reale pe axa numerelor
- • Operații cu numere reale
- • Adunarea și scăderea
- • Înmulțirea
- • Împărțirea
- • Puteri cu exponent număr întreg
- • Reguli de calcul cu radicali
- • Ordinea efectuării operațiilor
- • Raționalizarea numitorului (prima parte) de forma \({a\sqrt{b}}\)
- • Media geometrică (proporțională) a două numere reale pozitive
- • Media aritmetică ponderată
- • Ecuații de forma \({x^2 = a \in \mathbf{R}}\)
- 11. Ecuaţii şi
sisteme de ecuaţii liniare - • Transformarea unei egalități într-o egalitate echivalentă. Identități
- • Ecuații de forma \({ax + b = 0 }\), \({a, b \in \mathbf{R}}\)
- • Sisteme de două ecuații liniare cu două necunoscute
- • Metoda substituției
- • Metoda reducerii
- • Probleme care se rezolvă cu ajutorul ecuațiilor
- • Probleme care se rezolvă cu ajutorul sistemelor de ecuații
- 12. Intervale de numere reale
- • Mulțimi definite printr-o proprietate comună a elementelor lor
- • Intervale de numere reale
- • Explicitarea modulului
- • Partea întreagă. Partea fracționară
- • Operații cu intervale
- 13. Inecuaţii în \({\mathbf{R}}\)
- • Relația de inegalitate pe mulțimea numerelor reale
- • Inecuații de forma \({ax + b \ge 0 }\) (\({\le, <, > }\)), \({a, b \in \mathbf{R}}\)
- • Probleme care se rezolvă cu ajutorul inecuațiilor
- 14. Calcul algebric în \({\mathbf{R}}\)
- • Expresii algebrice
- • Operații cu numere reale reprezentate prin litere
- • Adunarea și scăderea
- • Înmulțirea, împărțirea, ridicarea la putere
- • Formule de calcul prescurtat
- • Raționalizarea numitorului - partea a doua
- • Descompuneri în factori
- • Fracții algebrice
- • Ce sunt fracțiile algebrice
- • Amplificarea și simplificarea fracțiilor algebrice
- • Operații cu fracții algebrice
- • Adunarea și scăderea fracțiilor algebrice
- • Înmulțirea fracțiilor algebrice
- • Împărțirea fracțiilor algebrice
- • Ridicarea la putere a fracțiilor algebrice
- 15. Ecuația de gradul 2
- • Forma, rezolvarea, discuția ecuației de gradul 2
- • Descompunerea în factori
- • Relațiile lui Viète
- • Ecuații bipătrate
- 16. Funcţia de gradul 1
- • Ce sunt funcțiile
- • Graficul unei funcții. Reprezentarea geometrică a graficului
- • Funcția de gradul 1 - definită pe \({\mathbf{R}}\)
- • Definită pe un interval mărginit
- • Definită pe un interval nemărginit
- • Definită pe o mulțime finită
- 17. Elemente de organizare
a datelor - • Organizarea datelor. Tabele. Frecvențe
- • Grafice
- • Grafice cu bare verticale (coloane)
- • Grafice cu bare orizontale (benzi)
- • Grafice cu linii
- • Diagrame circulare
- • Indicatorii tendinței centrale
- • Media
- • Mediana
- • Modul și amplitudinea
- • Probabilități
- • Produs cartezian
- • Sistem de axe ortogonale
- • Distanța dintre două puncte știind coordonatele lor. Mijlocul unui segment
* * *
∎ Aducerea fracțiilor la același numitor - numitorul comun este un multiplu comun al numitorilor fracțiilor. Pentru calcule mai ușoare, e bine să fie cel mai mic multiplu comun al acestora.
Cum aducem fracțiile la același numitor:
- simplificăm fracțiile până obținem fracții ireductibile (dacă nu sunt deja ireductibile)
- calculăm cel mai mic multiplu comun al numitorilor - acesta va fi numitorul comun al fracțiilor
- amplificăm fiecare fracție cu câtul dintre numitorul comun (cel nou) și numitorul vechi al fracției respective
De exemplu, să aducem la același numitor fracțiile \({ \frac{24}{16}}\), \({ \frac{25}{30}}\) și \({ \frac{81}{72}}\). Observăm că nu sunt ireductibile, deci le vom simplifica atât cât se poate.

Cel mai mic multiplu comun al numitorilor 2, 6 și 8 este 24. Acesta este numitorul comun.

Amplificăm fracția \({ \frac{3}{2}}\) cu rezultatul împărțirii lui 24 (numitorul comun) la 2 (numitorul fracției). Amplificăm fracția \({ \frac{5}{6}}\) cu rezultatul împărțirii lui 24 (numitorul comun) la 6 (numitorul fracției). Amplificăm fracția \({ \frac{9}{8}}\) cu rezultatul împărțirii lui 24 (numitorul comun) la 8 (numitorul fracției).

Observații:
- dacă numitorii fracțiilor sunt primi între ei (au un singur divizor comun, pe 1), atunci amplificăm fiecare fracție cu numitorul celeilalte fracții. De exemplu, să aducem la același numitor fracțiile \({ \frac{3}{7}}\) și \({ \frac{13}{12}}\). Numitorii 7 și 12 sunt primi între ei, deci vom amplifica prima fracție cu 12, iar pe a doua cu 7. Numitorul comun este 84 (7 înmulțit cu 12).
- dacă avem mai mult de două fracții cu numitorii primi între ei, amplificăm fiecare fracție cu produsul numitorilor celorlalte fracții