∎ Inecuații de forma \({ax + b \ge 0 }\) (\({\le, <, > }\)), \({a, b \in \mathbf{R}}\), \({x \in \mathbf{D}}\)

Inecuația de forma \({ax + b \ge 0 }\) (\({\le, <, > }\)), \({x \in \mathbf{D}}\) se numește inecuație liniară (de gradul 1) cu necunoscuta \({x}\).

• \({a}\) este coeficientul necunoscutei;
• \({b}\) este termenul liber;
• \({\mathbf{D}}\) este mulțimea în care necunoscuta ia valori;
• a rezolva o inecuație înseamnă a găsi valorile din mulțimea \({\mathbf{D}}\) ale necunoscutei \({x}\) pentru care inegalitatea este adevărată (aceste valori sunt soluții ale inecuației);
• pentru a găsi mulțimea soluțiilor unei inecuații (notată cu \({\mathbf{S}}\)), intersectăm mulțimea \({\mathbf{D}}\) cu mulțimea valorilor pentru care inecuația este adevărată;
• inecuația nu are o singură soluție, ci o mulțime de soluții; mulțimea soluțiilor poate fi o mulțime finită sau o mulțime infinită sau un interval, în funcție de mulțimea \({\mathbf{D}}\) în care necunoscuta ia valori;
• două inecuații care au aceeași mulțime a soluțiilor se numesc inecuații echivalente.

★ Când rezolvăm o inecuație, scopul este să separăm termenii: într-un membru termenii care conțin necunoscuta, iar în celălalt membru termenii liberi. Se obțin succesiv inecuații echivalente cu cea dată, astfel încât la final să putem deduce mulțimea soluțiilor.

★ Rezolvarea inecuației care are forma \({ax + b \ge 0 \;\;\;(\le, <, > )}\), cu \({x \in \mathbf{R}}\)

• îl trecem pe \({+b}\) în membrul drept, cu semn schimbat (adică îl scădem pe \({b}\) din ambii membri);



\({ax \ge -b }\)



• împărțim ambii membri cu \({a}\) (coeficientul necunoscutei \({x}\));

! ! ! contează dacă \({a}\) este pozitiv sau negativ




\({ax \ge -b \;\;\; \mid \;\;\; : a}\)



• dacă \({a>0}\), atunci \({x \ge -\frac{\displaystyle b}{\displaystyle a} }\), adică \({x \in \left[-\frac{\displaystyle b}{\displaystyle a}, + \infty \right) }\)






sau



• dacă \({a<0}\), atunci \({x \le -\frac{\displaystyle b}{\displaystyle a} }\), adică \({x \in \left(-\infty, -\frac{\displaystyle b}{\displaystyle a} \right] }\)

★Dacă inecuația nu are forma generală, atunci folosim proprietățile relației de inegalitate pe mulțimea numerelor reale pentru a o aduce la forma generală. Concret, avem următoarele reguli:

• trecerea unui termen dintr-un membru în altul se face cu semn schimbat, obținându-se o inecuație echivalentă cu cea dată;
• dacă înmulțim sau împărțim ambii membri cu un număr pozitiv, obținem o inecuație echivalentă cu cea dată;
• dacă înmulțim sau împărțim ambii membri cu un număr negativ, se schimbă sensul inegalității, obținându-se o inecuație echivalentă cu cea dată;
• dacă adunăm sau scădem același număr din ambii membri, obținem o inecuație echivalentă cu cea dată.

★ Dacă inecuația de rezolvat este o fracție comparată cu 0, cu necunoscuta \({x}\) doar la numitor sau doar la numărător, atunci trebuie să ne amintim regula semnelor:

• un număr negativ supra un număr pozitiv ne dă un număr negativ;
• un număr pozitiv supra un număr negativ ne dă un număr negativ;
• un număr pozitiv supra un număr pozitiv ne dă un număr pozitiv;
• un număr negativ supra un număr negativ ne dă un număr pozitiv.

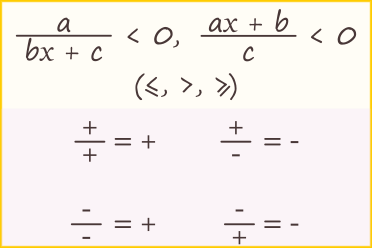
★ Dacă inecuația de rezolvat este de forma \({\mid ax + b \mid \le 0}\), folosim proprietățile modulului unui număr real:

\({|x| \le a }\) este echivalent cu \({x \in [-a, a] }\) este echivalent cu \({-a \le x \le a }\)

\({|x| < a }\) este echivalent cu \({x \in (-a, a) }\) este echivalent cu \({-a < x < a }\)

★ Exemple

1. Rezolvați în \({\mathbf{Z}}\), apoi în \({\mathbf{R}}\) inecuația \({5x + 4 \le 9x + 3}\).

• separăm termenii:

\({5x - 9x \le - 4 + 3}\)

• efectuăm calculele în fiecare membru:

\({- 4x \le - 1 \;\;\; \mid \; : (-4)}\)

• împărțim cu coeficientul necunoscutei (este -4, număr negativ, deci se schimbă sensul inegalității)

\({x \ge \frac{\displaystyle 1}{\displaystyle 4}}\)

\({x \in \left[\frac{\displaystyle 1}{\displaystyle 4}, + \infty \right) }\)

• soluția inecuației în \({\mathbf{Z}}\):

\({S = \mathbf{Z} \cap \left[\frac{\displaystyle 1}{\displaystyle 4}, + \infty \right) }\)

\({S = \{1, 2, 3, 4, ... \}}\)

• soluția inecuației în \({\mathbf{R}}\):

\({S = \mathbf{R} \cap \left[\frac{\displaystyle 1}{\displaystyle 4}, + \infty \right) }\)

\({S = \left[\frac{\displaystyle 1}{\displaystyle 4}, + \infty \right) }\)

2. Rezolvați în \({\mathbf{R}}\) inecuația \({\frac{\displaystyle 3}{\displaystyle 2x + 1} \le 0}\).

• numitorul fracției tebuie să fie diferit de 0:

\({2x + 1 \neq 0}\)

\({x \neq -\frac{\displaystyle 1}{\displaystyle 2}}\)

• numărătorul fracției este 3, număr pozitiv;

\({3>0}\)

• fracția nu poate fi 0, pentru că numărătorul este strict pozitiv;
• pentru ca fracția să fie mai mică decât 0, este necesar ca numitorul să fie mai mic decât 0:

\({2x + 1 < 0}\) - rezolvăm această inecuație

• separăm termenii:

\({2x < -1\;\;\; \mid \; : 2}\)

• împărțim ambii membri cu 2 (cu coeficientul necunoscutei):

\({x < -\frac{\displaystyle 1}{\displaystyle 2}}\)

\({x \in \left(-\infty, -\frac{\displaystyle 1}{\displaystyle 2} \right) }\)

• soluția inecuației:

\({S = \mathbf{R} \cap \left(-\infty, -\frac{\displaystyle 1}{\displaystyle 2} \right) }\)

\({S = \left(-\infty, -\frac{\displaystyle 1}{\displaystyle 2} \right)}\)

3. Rezolvați în \({\mathbf{R}}\) inecuația \({\left|\frac{\displaystyle 2 - 3x}{\displaystyle 5}\right| \le \frac{\displaystyle 2}{\displaystyle 3}}\).

• folosim proprietatea modulului:



\({|x| \le a }\) este echivalent cu \({x \in [-a, a] }\) este echivalent cu \({-a \le x \le a }\);




\({\left|\frac{\displaystyle 2 - 3x}{\displaystyle 5}\right| \le \frac{\displaystyle 2}{\displaystyle 3}}\) \({ \Longleftrightarrow}\) \({\frac{\displaystyle 2 - 3x}{\displaystyle 5} \in \left[-\frac{\displaystyle 2}{\displaystyle 3}, \frac{\displaystyle 2}{\displaystyle 3}\right] }\) \({ \Longleftrightarrow}\) \({-\frac{\displaystyle 2}{\displaystyle 3} \le \frac{\displaystyle 2 - 3x}{\displaystyle 5} \le \frac{\displaystyle 2}{\displaystyle 3} }\);



• rezolvăm inecuația \({-\frac{\displaystyle 2}{\displaystyle 3} \le \frac{\displaystyle 2 - 3x}{\displaystyle 5} \le \frac{\displaystyle 2}{\displaystyle 3} }\)


• înmulțim inecuația cu cel mai mic multiplu comun al numitorilor celor două fracții (vrem să scăpăm de numitori):




\({-\frac{\displaystyle 2}{\displaystyle 3} \le \frac{\displaystyle 2 - 3x}{\displaystyle 5} \le \frac{\displaystyle 2}{\displaystyle 3} \;\;\; \mid \; \cdot \; 15}\)




\({-\frac{\displaystyle 2}{\displaystyle \cancel{3}} \cdot \cancel{15}^5 \le \frac{\displaystyle 2 - 3x}{\displaystyle \cancel{5}} \cdot \cancel{15}^3 \le \frac{\displaystyle 2}{\displaystyle \cancel{3}} \cdot \cancel{15}^5}\)




\({-10 \le 3(2 - 3x)\le 10}\)




\({-10 \le 6 - 9x \le 10 \;\;\; \mid \; - \; 6}\)



• scădem 6 din toți membrii:



\({-10 - 6 \le - 9x \le 10 - 6}\)




\({-16 \le - 9x \le 4 \;\;\; \mid \; : \; (-9)}\)



• împărțim cu -9 toți membrii (se schimbă sensul inegalităților):



\({\frac{\displaystyle 16}{\displaystyle 9} \ge x \ge -\frac{\displaystyle 4}{\displaystyle 9} }\)




\({x \in \left[-\frac{\displaystyle 4}{\displaystyle 9}, \frac{\displaystyle 16}{\displaystyle 9} \right] }\)

• soluția inecuației:



\({S = \mathbf{R} \cap \left[-\frac{\displaystyle 4}{\displaystyle 9}, \frac{\displaystyle 16}{\displaystyle 9} \right] }\)




\({S = \left[-\frac{\displaystyle 4}{\displaystyle 9}, \frac{\displaystyle 16}{\displaystyle 9} \right]}\)



• inecuația \({-\frac{\displaystyle 2}{\displaystyle 3} \le \frac{\displaystyle 2 - 3x}{\displaystyle 5} \le \frac{\displaystyle 2}{\displaystyle 3} }\) poate fi „spartă” în două inecuații:


• \({-\frac{\displaystyle 2}{\displaystyle 3} \le \frac{\displaystyle 2 - 3x}{\displaystyle 5} }\) cu mulțimea soluțiilor \({S_1 = \left(- \infty, \frac{\displaystyle 16}{\displaystyle 9} \right] }\)



• \({\frac{\displaystyle 2 - 3x}{\displaystyle 5} \le \frac{\displaystyle 2}{\displaystyle 3} }\) cu mulțimea soluțiilor \({S_2 = \left[-\frac{\displaystyle 4}{\displaystyle 9}, + \infty \right) }\)



• \({S = S_1 \cap S_2 = \left[-\frac{\displaystyle 4}{\displaystyle 9}, \frac{\displaystyle 16}{\displaystyle 9} \right] }\)

Exersează!

Exersează 1 | Exersează 2

Dacă vreți să susțineți funcționarea și dezvoltarea mathema.ro, puteți contribui prin donație. Aceasta nu elimină reclamele existente, dar îmi permite să accelerez dezvoltarea website-ului și să acopăr costurile de funcționare.

Nume titular: GEORGIU LIVIA-NICOLETA

IBAN: RO20BTRLRONCRT0287588001

SWIFT: BTRLRO22

Mulțumesc! ❤️