facebook | mathema.romania@gmail.com
Memorator Algebră
clasele 5 - 8
∎ Adunarea și scăderea numerelor reale
* * *
Numerele care se adună se numesc termeni. Rezultatul adunării se numește sumă.
Scăderea poate fi privită ca o adunare, astfel:
\({a - b = a + (-b)}\), unde \({-b}\) este opusul lui \({b}\)
- Suma a două numere raționale este un număr rațional.
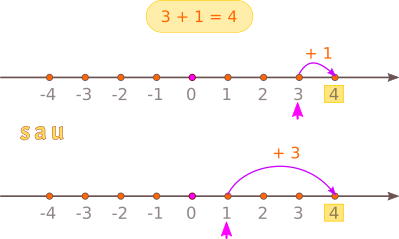
- Suma a două numere pozitive este un număr pozitiv:
- Suma a două numere negative este un număr negativ:
- Suma dintre un număr pozitiv și un număr negativ:
- numărul pozitiv are modulul mai mare - suma este număr pozitiv
- numărul negativ are modulul mai mare - suma este număr negativ
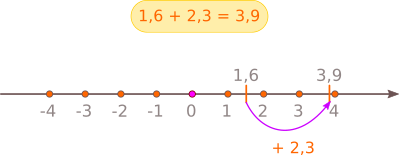

\({a - b = a + (-b) = -b + a}\), unde \({-b}\) este opusul lui \({b}\)


Reținem!

- Suma dintre un număr rațional și un număr irațional este un număr irațional.
- pentru a efectua calculul, folosim o aproximare a numărului irațional
\({2 + \sqrt{3} = 2 + 1{,}73 = 3{,}73}\)
\({\sqrt{3} \approx 1{,}73}\)
- Suma dintre două numere iraționale poate fi un număr irațional sau un număr rațional.
- \({\underbrace{2 + \cancel{\sqrt{3}}}_{irațional} - \underbrace{\cancel{\sqrt{3}}}_{irațional} = 2 \in ℚ}\)
- \({\underbrace{3 + \sqrt{2}}_{irațional} + \underbrace{1 -2\sqrt{2}}_{irațional} = 4 - \sqrt{2} \in ℝ - ℚ}\)
- numerele raționale 3 și 1 sunt termeni asemenea și se adună
- numerele iraționale \({\sqrt{2}}\) și \({-2\sqrt{2}}\) sunt termeni asemenea și se adună
- \({10 + \sqrt{5} + 1 -3\sqrt{2} = 11 + \sqrt{5} -3\sqrt{2} \in ℝ - ℚ}\)
- numerele raționale 10 și 1 sunt termeni asemenea și se adună
- numerele iraționale \({\sqrt{5}}\) și \({-3\sqrt{2}}\) nu sunt termeni asemenea și nu se adună
- dacă e posibil și folositor, se introduc sau se scot termenii (de) sub radical
- \({3 + 3\sqrt{2} + \sqrt{8} - 5 = }\)
- \({5 + 2\sqrt{3} - \sqrt{12} = }\)
- putem folosi aproximări pentru numerele iraționale
- \({\sqrt{2} + \sqrt{3} = 1{,}41 + 1{,}73 = 3{,}14}\)
termenii numere raționale sunt asemenea și se adună
\({2\sqrt{2} = \underbrace{\sqrt{2} + \sqrt{2}}_{\text{de} \; \text{două} \; \text{ori}} }\)
\({n\sqrt{a} = \underbrace{\sqrt{a}\; + \;... \;+\; \sqrt{a}}_{\text{de} \; \text{n} \; \text{ori}} }\)
\({m\sqrt{a}}\) și \({n\sqrt{a}}\) sunt termeni asemenea și se adună
\({m\sqrt{a} + n\sqrt{a} = (m + n)\sqrt{a}}\)
\({m\sqrt{a} - n\sqrt{a} = (m - n)\sqrt{a}}\)
\({\sqrt{2} - 2\sqrt{2} = (1 - 2)\sqrt{2} = -\sqrt{2}}\)
\({\sqrt{a} + \sqrt{b} \neq \sqrt{a + b} }\)
\({= -2 + 3\sqrt{2} + 2\sqrt{2} }\)
\({= -2 + 5\sqrt{2} }\)
\({= 5 + \cancel{\sqrt{12}} - \cancel{\sqrt{12} }}\)
\({= 5}\)
- Pentru \({a }\) și \({b}\) numere raționale și \({\sqrt{x}}\) număr irațional, avem:
- Dacă \({a + b\sqrt{x} = 0}\), atunci \({a = 0}\) și \({b = 0}\)
- Dacă \({a + b\sqrt{x} = 1}\), atunci \({a = 1}\) și \({b = 0}\)
- Dacă \({a + b\sqrt{x} = \sqrt{x}}\), atunci \({a = 0}\) și \({b = 1}\)
- Dacă \({a + b\sqrt{x} = b\sqrt{x}}\), atunci \({a = 0}\)
- Pentru \({a }\), \({b}\), \({a' }\), \({b'}\) numere raționale și \({\sqrt{x}}\) număr irațional, avem:
- Dacă \({a + b\sqrt{x} = a' + b'\sqrt{x}}\), atunci \({a = a'}\) și \({b = b'}\)
- Dacă \({a = a'}\) și \({b = b'}\), atunci \({a + b\sqrt{x} = a' + b'\sqrt{x}}\)
- Semnul - (minus) în fața parantezei schimbă semnul termenilor din paranteză
- \({3 - (2 + 5\sqrt{5}) = 3 - 2 - 5\sqrt{5} = 1 - 5\sqrt{5}}\)
- Proprietățile adunării numerelor reale
- adunarea este comutativă
- adunarea este asociativă
- 0 este element neutru la adunare
- orice număr real are un opus
\({a + b = b + a}\)
\({3 + \sqrt{5} = \sqrt{5} + 3}\)
\({-2 + \sqrt{2} = \sqrt{2} - 2}\)
\({-1 - 2\sqrt{2} = -2\sqrt{2} - 1}\)
\({(a + b) + c = a + (b + c) = (a + c) + b}\)
\({3 + \sqrt{2} + 4 + 2\sqrt{2}=}\)
\({= 3 + 4 + \sqrt{2} + 2\sqrt{2}}\)
\({= 7 + 3\sqrt{2}}\)
\({a + 0 = 0 + a = a}\)
\({a + (-a) = (-a) + a = 0}\)
\({2 - 2\sqrt{5} + 2\sqrt{5} = 2}\)
opusul lui \({a + b\sqrt{x}}\) este \({-(a + b\sqrt{x}) = -a - b\sqrt{x}}\)
☑ Opusul unui număr rațional este tot un număr rațional.
☑ Opusul unui număr irațional este tot un număr irațional.
