facebook | mathema.romania@gmail.com
Memorator Algebră
clasele 5 - 8
∎ Expresii algebrice
Expresia algebrică (pe scurt, expresia) este o înșiruire de operații cu numere cunoscute și necunoscute. Numerele necunoscute se notează cu litere și se mai numesc variabile sau nedeterminate. Expresia este dependentă de variabilele sale.
Expresia algebrică este o generalizare a unei situații concrete. Înlocuind variabilele cu numere date, se obțin valori numerice ale expresiei.
Expresia algebrică se notează cu o literă mare, de obicei litera E, urmată de paranteză rotundă în care scriem variabila sau variabilele de care depinde expresia.
Reținem!
Un produs algebric este un produs în care unul sau mai mulți factori sau toți factorii sunt variabile (necunoscute) reprezentate prin litere.
O sumă algebrică este o succesiune de adunări și scăderi în care termenii sunt produse algebrice.
Produsele și sumele algebrice sunt expresii algebrice.
Exemple
1. Un caiet costă 3 lei. Cât costă 10 caiete?
10 caiete costă \({10 \cdot 3}\) lei, adică 30 de lei.
1'. Un caiet costă \({x}\) lei. Cât costă 10 caiete?
10 caiete costă \({10 \cdot x}\) lei, adică \({10x}\) lei.
Prețul unui caiet l-am notat cu o literă pentru că nu-l știm. Astfel am obținut o expresie algebrică, sau, pe scurt, expresie: \({10x}\).
Necunoscuta \({x}\) se mai numește variabilă sau nedeterminată.
O expresie algebrică cu o singură variabilă se notează cu o literă (de obicei cu litera E), urmată în paranteză de variabila respectivă. Putem scrie:
\({E(x) = 10x}\)
Citim: „E de \({x}\) este egal cu 10 \({x}\)” (expresia E este dependentă de variabila \({x}\)).
Produsul \({10x}\) se mai numește produs algebric, pentru că unul dintre factori este înlocuit cu o literă (numerele care se înmulțesc se numec factori, iar rezultatul înmulțirii se numește produs). Semnul operației de înmulțire se omite. Factorul cunoscut se numește coeficient, iar factorii necunoscuți formează partea literală.

Atunci când coeficientul produsului este egal cu 1, acesta nu se mai scrie. De exemplu, în loc de \({1x}\) scriem și înțelegem \({x}\).
Dacă produsul are coeficientul egal cu -1, se păstrează doar semnul minus. De exemplu, în loc de \({-1x}\) scriem și înțelegem \({-x}\).
Când variabilele (literele) sunt înlocuite cu numere și se efectuează calculele, obținem valoarea numerică a expresiei.
De exemplu, \({E(3) = 10 \cdot 3 = 30}\) sau \({E(4{,}5) = 10 \cdot 4{,}5 = 45}\).
2. Ileana are 3 livezi cu meri; fiecare livadă are 10 rânduri, iar pe fiecare rând sunt 24 de meri. Câți meri sunt în total?
În total sunt \({3 \cdot 10 \cdot 24 }\) de meri, adică 720 de meri.
2'. Ileana are 3 livezi cu meri și încă 5 meri lângă casă; fiecare livadă are \({x}\) rânduri, iar pe fiecare rând sunt \({y}\) meri. Câți meri sunt în total?
În total sunt \({3 \cdot x \cdot y + 5}\) de meri, adică \({3xy + 5}\) meri.
Am obținut expresia algebrică \({E(x, y) = 3xy + 5}\), dependentă de variabilele \({x}\) și \({y}\).
Citim: „E de \({x}\) și \({y}\) este egal cu 3 \({x}\) \({y}\) plus 5”. Avem o sumă algebrică în care unul dintre termeni este produsul \({3xy}\), iar celălalt termen este +5. Termenul care nu conține nicio variabilă se numește termen liber.

3. Calculează aria totală.
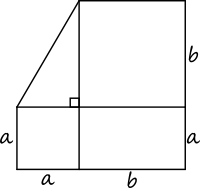
Avem:
- un pătrat cu latura \({a}\);
- un pătrat cu latura \({b}\);
- un dreptunghi cu laturile \({a}\) și \({b}\);
- un triunghi dreptunghic cu catetele \({a}\) și \({b}\).
Aria totală este \({\mathcal{A} = a^2 + b^2 + ab + \frac{\displaystyle ab}{\displaystyle 2}}\).
Am obținut o expresie algebrică dependentă de variabilele \({a}\) și \({b}\):
\({E(a, b) = a^2 + b^2 + ab + \frac{\displaystyle ab}{\displaystyle 2}}\)
Aceasta este o sumă algebrică în care termenii sunt produsele \({a^2}\), \({b^2}\), \({ab}\) și \({\frac{\displaystyle ab}{\displaystyle 2}}\).
Produsele \({a^2}\), \({b^2}\), \({ab}\) au coeficientul 1 (acesta nu se mai scrie).
Produsul \({\frac{\displaystyle ab}{\displaystyle 2}}\) are coeficientul \({\frac{\displaystyle 1}{\displaystyle 2}}\).
