facebook | mathema.romania@gmail.com
Memorator Algebră
clasele 5 - 8
∎ Organizarea datelor. Tabele. Frecvențe
★ se obțin datele prin anchete, sondaje sau alte metode statistice;
★ pentru a fi mai ușor de citit și analizat, datele se scriu într-un tabel;
★ pe baza tabelului, se construiesc grafice și diagrame;
★ se analizează datele, se calculează indicatori statistici;
★ se formulează concluziile.
∎ Primul exemplu
La începutul anului școlar, elevii clasei a V-a dau un test inițial matematică; se obțin următoarele note: Alina obține nota 9, Mihai - nota 6, Radu - nota 5, Andrei - nota 8, Mihaela - nota 6, Raluca - nota 10, Mihnea - nota 8, Daria - nota 10, Maria - nota 5, Răzvan - nota 7, Marius nota 10, Gabriel - nota 7, Darius - nota 9, Ilinca - nota 7, Irina - nota 9, Nicușor - nota 8, Marina - nota 7, Vlad - nota 9, Ramona - nota 7, Monica - nota 7, Robert - nota 8.
Toți elevii pe care se face cercetarea formează populația statistică. Fiecare elev este considerat unitate statistică sau individ; își pierde identitatea, singurul lucru care contează pentru statistică este trăsătura comună a participanților la cercetare.
Toți elevii clasei (Alina, Mihai, Radu, Andrei etc.) au o trăsătură comună: nota obținută la test. Această trăsătură comună se numește caracteristică sau variabilă.
Variabila (trăsătura comună) ia valori. În cazul nostru, valorile notei sunt 5, 6, 7, 8, 9 și 10. Observăm că valorile acestea sunt numere; spunem că variabila „nota obținută” ia valori numerice. Variabila poate avea valori numerice sau însușiri. În exemplul următor vom avea o variabilă cu valori calitative (însușiri).
Numărul natural care ne arată de câte ori apare variabila cercetată se numește frecvența absolută a variabilei respective (putem să spunem simplu, frecvența).
Frecvența relativă (calculată ca fracție sau procent) este raportul dintre frecvența absolută a unei valori a variabilei și totalul populației statistice.
Dacă vrem să analizăm notele obținute la nivelul întregii clase, ele sunt greu de analizat scrise în această formă. De aceea, le scriem sub forma unui tabel de date. Astfel, avem o imagine clară a notelor obținute. Dacă tabelul conține frecvențe, atunci el se mai numește tabel de frecvențe)
Tabelul poate fi organizat pe rânduri sau pe coloane. Avem exemple puțin mai jos.
Tabelul trebuie să aibă un titlu general, care să ne indice despre ce este vorba în cuprinsul lui; rândurile (sau coloanele) au nevoie de titlu; acesta se scrie la capătul din stânga al rândului (sau la capătul de sus al coloanei).
Să vedem tabelul care prezintă situația notelor obținute de elevii clasei a V-a.
- am organizat tabelul pe rânduri;
- este un tabel al frecvențelor, pentru că pe a doua linie am scris frecvența notelor;
- titlul general este „Situația notelor la matematică, test inițial, clasa a V-a”;
- titlul primului rând este „Nota” (pe acest rând scriem notele obținute, în cazul nostru vor fi notele de la 5 la 10);
- titlul celui de-al doilea rând este „Numărul elevilor” (pe acest rând scriem câți elevi au obținut nota o anumită notă; de exemplu sub nota 5 vom scrie 2, pentru că 2 elevi au nota 5).

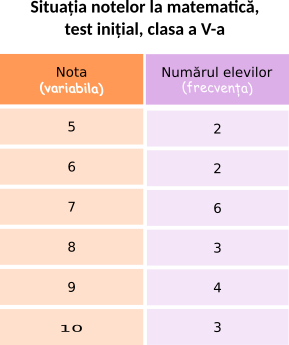
Observăm că în tabel nu am scris numele elevilor. Pe prima linie a tabelului am scris nota - elevii au obținut note de la 5 la 10, deci am scris notele 5, 6, 7, 8, 9 și 10. Pe a doua linie am scris câți elevi au obținut fiecare notă: 2 elevi au obținut nota 5, deci sub 5 scriem 2; 2 elevi au obținut nota 6, deci sub 6 scriem 2; 6 elevi au obținut nota 7, deci sub 7 scriem 6; 3 elevi au obținut nota 8, deci sub 8 scriem 3; 4 elevi au obținut nota 9, deci sub 9 scriem 4; 3 elevi au obținut nota 10, deci sub 10 scriem 3.
Observăm că pe prima linie a tabelului de date avem valorile variabilei, iar pe a doua linie avem frecvențele.
- Nota 5 a fost obținută de 2 elevi. Spunem că frecvența absolută a notei 5 este 2.
- Nota 8 a fost obținută de 3 elevi. Spunem că frecvența absolută a notei 8 este 3.
Dacă ne raportăm la numărul total de elevi, putem calcula frecvența relativă a notelor. În total sunt 20 de elevi.
- De exemplu, \({\frac{\displaystyle 2}{\displaystyle 20}}\), adică \({10 \%}\) reprezintă frecvența relativă a notei 6 (numărul elevilor care au obținut nota 6 supra numărul total al elevilor).
- Frecvența relativă a notei 9 este \({\frac{\displaystyle 4}{\displaystyle 20}}\), adică \({20 \%}\) din totalul notelor (numărul elevilor care au obținut nota 9 supra numărul total al elevilor).
Observație! Tabelul frecvențelor se poate scrie sub formă de coloane, astfel:
∎ Al doilea exemplu
12 copii de clasa a V-a și-au ales activitățile extrașcolare astfel: Maria participă la cursul de dans, Ionel la cursul de șah, Victoria merge la volei, Alex participă la fotbal, Mioara la șah, Amelia la fotbal, Raluca la volei, Robert merge la fotbal, Irina merge la dans, Florina merge la volei, Viorel și Mihai merg la dans.
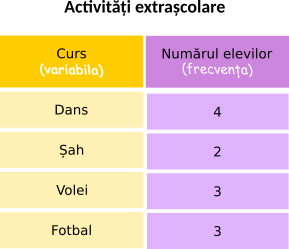
Grupăm aceste date într-un tabel. Trăsătura comună a celor 12 copii este faptul că participă la un curs. Aceasta este variabila. Ea poate să ia valorile: dans, șah, volei și fotbal. Pe prima linie a tabelului scriem valorile variabilei, pe a doua linie a tabelului scriem câți copii participă la fiecare curs (frecvența).
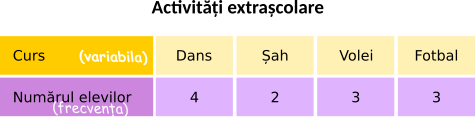
Observăm că valorile variabilei nu mai sunt numere, ca în primul exemplu.
Să vedem care sunt frecvențele absolute (sunt cele de pe a doua linie a tabelului). Frecvența absolută este un număr natural.
- frecvența la cursul de dans este 4;
- frecvența la cursul de șah este 2;
- frecvența la cursul de volei este 3;
- frecvența la cursul de fotbal este 3.
Să vedem care sunt frecvențele relative (calculate ca fracții sau procente). Se calculează ca raport între frecvența absolută a unei valori a variabilei și totalul populației statistice. În cazul nostru, populația statistică e formată din cei 12 elevi.
- frecvența relativă la cursul de dans este \({\frac{\displaystyle 4}{\displaystyle 12}}\), adică \({33\%}\)
- frecvența relativă la cursul de șah este \({\frac{\displaystyle 2}{\displaystyle 12}}\), adică aproximativ \({17\%}\);
- frecvența relativă la cursul de volei este \({\frac{\displaystyle 3}{\displaystyle 12}}\), adică \({25\%}\);
- frecvența relativă la cursul de fotbal este \({\frac{\displaystyle 3}{\displaystyle 12}}\), adică \({25\%}\).
Observație! Tabelul frecvențelor se poate scrie sub formă de coloane, astfel: