∎ Modulul unui număr real

Modulul unui număr real sau valoarea absolută a unui număr real este distanța de la originea axei numerelor reale la punctul de pe axă corespunzător numărului respectiv.

Modulul unui număr real este întotdeauna pozitiv, pentru că el măsoară o distanță.

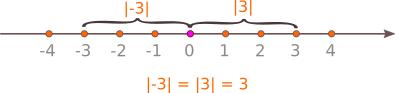
Scriem \({|x|}\) și citim „modul de \({x}\)”.

Explicitarea modulului:

• modulul unui număr pozitiv este egal cu numărul respectiv;
• modulul unui număr negativ este egal cu opusul numărului respectiv (două numere sunt opuse dacă au același modul și unul este pozitiv, iar celălalt este negativ);
• modulul lui 0 este egal cu 0;
• dacă \({a > 0}\) și \({x \in \mathbf{R}}\), avem:
• \({|x| = a }\) este echivalent cu \({x \in \{-a, a \} }\);
• \({|x| \le a }\) este echivalent cu \({x \in [-a, a] }\) este echivalent cu \({-a \le x \le a }\);
• \({|x| < a }\) este echivalent cu \({x \in (-a, a) }\) este echivalent cu \({-a < x < a }\);
• \({|x| \ge a }\) este echivalent cu \({x \in (- \infty, -a] \cup [a, + \infty) }\);
• \({|x| > a }\) este echivalent cu \({x \in (- \infty, -a) \cup (a, + \infty) }\).

Proprietățile modulului unui număr real sunt aceleași cu proprietățile modulului unui număr rațional.

• \({|x| = x}\), pentru \({x > 0}\);
• \({|x| = -x}\), pentru \({x < 0}\);
• \({|x| = 0}\) dacă și numai dacă \({x = 0}\);
• \({|x| \ge 0}\), pentru orice \({x}\) număr real;
• \({|x| = |-x|}\), pentru orice \({x}\) număr real;
• \({\sqrt{x^2} = |x|}\), pentru orice \({x}\) număr real;
• \({|x + y| \le |x| + |y|}\), pentru orice \({x}\) și \({y}\) numere reale (inegalitatea triunghiului);
• \({|x \cdot y| = |x| \cdot |y|}\), pentru orice \({x}\) și \({y}\) numere reale;
• \({\left|\frac{x}{y}\right|}\) \({=}\) \({\frac{|x|}{|y|}}\), pentru orice \({x}\) și \({y}\) numere reale și \({y \neq 0}\);
• \({|x^n| = |x|^n}\), pentru orice \({x}\) număr real și \({n}\) număr natural;
• \({|x| \le a}\) dacă și numai dacă \({-a \le x \le a}\);

\({|x| < a}\) dacă și numai dacă \({-a < x < a}\)

• \({||x| - |y|| \le |x - y|}\), pentru orice \({x}\) număr real.

Exersează 1

Dacă vreți să susțineți funcționarea și dezvoltarea mathema.ro, puteți contribui printr-o donație singulară sau lunară. Aceasta nu elimină reclamele existente, dar îmi permite să accelerez dezvoltarea website-ului și să acopăr costurile de funcționare.

Nume titular: GEORGIU LIVIA-NICOLETA

IBAN: RO20BTRLRONCRT0287588001

SWIFT: BTRLRO22

Mulțumesc! ❤️