facebook | mathema.romania@gmail.com
Memorator Algebră
clasele 5 - 8
∎ Numerele întregi
Un număr întreg se reprezintă cu ajutorul unui număr natural precedat de semnul + (plus) sau - (minus). Numerele negative se folosesc, de exemplu, pentru măsurarea temperaturilor.
Mulțimea numerelor întregi se notează cu \({ℤ}\).
\({ℤ = \{..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ... \}}\) \({= \{0, ±1, ±2, ±3, ±4, ±5, ... \}}\)
- Numerele întregi care au semnul + sunt numere întregi pozitive și se identifică cu numerele naturale. De exemplu, +9 este număr întreg pozitiv și se citește „plus nouă”. Semnul + poate fi omis: +9 și 9 semnifică același număr.
- Numerele întregi care au semnul - sunt numere întregi negative. De exemplu, -5 este număr întreg negativ și se citește „minus cinci”.
\({ℤ_+ = \{1, 2, 3, 4, ... \}}\) \({= \{x ∈ ℤ \;| \; x>0\}}\) \({= ℕ^*}\) - mulțimea numerelor întregi pozitive
\({ℤ_- = \{..., -4, -3, -2, -1\}}\) \({= \{x ∈ ℤ \; |\; x<0\}}\) - mulțimea numerelor întregi negative
Mulțimea numerelor întregi nenule este \({ℤ^* = ℤ - \{0\}}\).
\({ℤ^*}\), \({ℤ_+}\) și \({ℤ_-}\) sunt submulțimi ale lui \({ℤ}\).
\({ℤ^* ⊂ ℤ}\)
\({ℤ_+ ⊂ ℤ}\)
\({ℤ_- ⊂ ℤ}\)
\({ℤ = ℤ_- ∪ \{0\} ∪ ℤ_+ }\)
Opusul unui număr întreg \({n}\) se notează cu \({-n}\). Opusul lui 15 este -15, iar opusul lui -24 este 24. Opusul lui 0 este 0.
Două numere întregi opuse diferă prin semnul lor.
Reprezentarea numerelor întregi pe axa numerelor
Axa numerelor este o dreaptă pe care considerăm un sens, o origine O și o unitate de măsură.
Numerele întregi pozitive sunt de fapt numerele naturale, pe care le reprezentăm în mod obișnuit pe axa numerelor. Pentru a reprezenta pe axă numerele întregi negative, ținem seama de faptul că un număr întreg negativ este opusul unui număr întreg pozitiv. Două numere întregi opuse se reprezintă pe axă prin puncte simetrice față de origine.
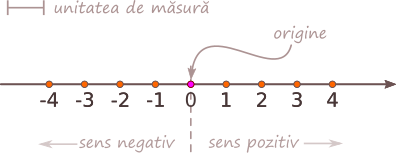
Pe axa numerelor, de la originea O spre dreapta avem sensul pozitiv al dreptei; toate numerele așezate pe axa numerelor în sensul pozitiv sunt numere pozitive, adică au semnul +. Aceste numere sunt mai mari decât 0.
Pe axa numerelor, de la originea O spre stânga avem sensul negativ al dreptei; toate numerele așezate pe axa numerelor în sensul negativ sunt numere negative, adică au semnul -. Aceste numere sunt mai mici decât 0.
Modulul unui număr întreg \({a}\) se notează cu \({|a|}\) și semnifică distanța de la origine până la punctul prin care este reprezentat numărul pe axa numerelor. Fiind o distanță, modulul unui număr întreg este întotdeauna mai mare decât 0.
\({|a| = |-a|}\) pentru orice număr întreg \({a}\) (modulele a două numere opuse sunt egale pentru că sunt reprezentate pe axa numerelor prin puncte simetrice față de origine, adică prin puncte egal depărtate de origine)
Observăm că:
- modulul unui număr întreg pozitiv este egal cu numărul respectiv: \({|62| = 62}\)
- modulul unui număr întreg negativ este egal cu opusul numărului respectiv: \({|-14| = -(-14) = 14}\)
- modulul lui 0 este egal cu 0: \({|0| = 0}\)

Compararea și ordonarea numerelor întregi
Atunci când comparăm două numere întregi, este mai mare cel care este reprezentat în dreapta pe axa numerelor.
- orice număr întreg negativ este mai mic decât orice număr întreg pozitiv: \({-34 < 10}\)
- orice număr întreg negativ este mai mic decât 0: \({-22 < 0}\)
- când comparăm două numere întregi negative, este mai mare cel care are modulul mai mic: \({-41 < -10}\)
- compararea a două numere întregi pozitive înseamnă, de fapt, compararea a două numere naturale: \({10 < 20}\)
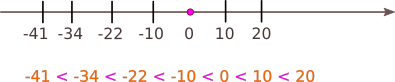
Exersează! Compararea numerelor întregi
Exersează! Modulul unui număr întreg
