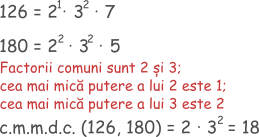Exersează ❙ 1
* * *
∎ Cel mai mare divizor comun (c.m.m.d.c.) al două sau mai multe numere naturale este cel mai mare număr natural care divide pe fiecare dintre numerele respective. Acesta ne ajută la găsirea factorului comun.
Cel mai mare divizor comun al numerelor \({a}\) și \({b}\) se notează cu \({(a, b)}\).
Dacă două numere \({a}\) și \({b}\) au un singur divizor comun, acesta fiind numărul 1, atunci ele se numesc numere prime între ele. Notăm \({(a, b)=1}\).
- de exemplu, numerele 12 și 25 sunt numere prime între ele pentru că numărul 1 este singurul lor divizor comun. Scriem \({(12, 25)=1}\)
Cum calculăm c.m.m.d.c. al unor numere naturale:
- se descompun numerele în factori primi la diferite puteri
- se înmulțesc între ei doar factorii comuni la puterea cea mai mică, luați o singură dată. Produsul obținut este cel mai mare divizor comun al numerelor.
Să calculăm cel mai mare divizor comun al numerelor 126 și 180.
- descompunem în factori primi numerele 126 și 180
- considerăm doar factorii comuni la puterea cea mai mică, luați o singură dată, adică 2 și 32. Produsul obținut este 18; acesta este cel mai mare divizor comun al numerelor 126 și 180.