∎ Paralelogramul este patrulaterul convex care are laturile opuse paralele două câte două.

★ Cum desenăm un paralelogram?

• desenăm două segmente paralele și congruente, unul puțin mai la stânga sau mai la dreapta; de preferat, segmentele să fie orizontale;
• unim capetele din stânga, apoi pe cele din dreapta;
• notăm vârfurile unul după celălalt, cu litere mari de tipar.

★ Proprietăți

• Laturile opuse sunt congruente (egale) și paralele două câte două.
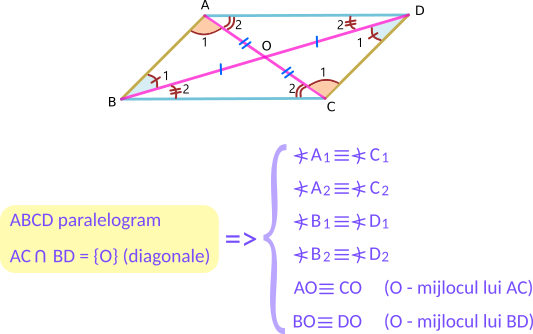
• Unghiurile opuse sunt congruente (egale) două câte două.
• Unghiurile alăturate sunt suplementare (au suma egală cu 180^o)



• Diagonalele se înjumătățesc.
• Unghiurile formate de o diagonală cu laturile opuse sunt egale.



• Punctul de intersecție a diagonalelor este centrul de simetrie al paralelogramului (simetricul fiecărui punct al paralelogramului față de intersecția diagonalelor se află pe paralelogram).

★ Cum arătăm că un patrulater convex e paralelogram

• Arătăm că două laturi opuse sunt paralele și congruente (egale).
• Arătăm că laturile opuse sunt paralele două câte două.
• Arătăm că laturile opuse sunt congruente (egale) două câte două.
• Arătăm că unghiurile opuse sunt congruente (egale) două câte două.
• Arătăm că unghiurile alăturate sunt suplementare două câte două.
• Arătăm că diagonalele se înjumătățesc.
• Arătăm că unghiurile formate de fiecare diagonală cu laturile opuse sunt egale.

★ Aria paralelogramului

Fie paralelogramul ABCD, cu AB paralelă cu CD și AD paralelă cu BC.

• înălțimea paralelogramului corespunzătoare laturii AD (sau BC) este distanța dintre laturile paralele AD și BC;



• înălțimea paralelogramului corespunzătoare laturii AB (sau CD) este distanța dintre laturile paralele AB și CD;



• aria paralelogramului este egală cu produsul dintre lungimea unei laturi și înălțimea corespunzătoare:





\({Aria = BC \cdot h_1}\)

\({\textcolor{white}{Aria}=AD \cdot h_1}\)

\({\textcolor{white}{Aria}=AB \cdot h_2}\)

\({\textcolor{white}{Aria}=CD \cdot h_2}\)

• alte formule pentru aria paralelogramului:
• fie \({d_1}\) și \({d_2}\) diagonalele paralelogramului;
• fie \({α}\) unghiul ascuțit dintre diagonalele paralelogramului;
• fie \({β}\) unghiul ascuțit dintre laturile paralelogramului.






\({Aria \; paralelogram= a \cdot b \cdot \text{sin} \; β }\)




\({Aria \; paralelogram= \frac {\displaystyle d_1 \cdot d_2 \cdot \text{sin} \; α}{\displaystyle 2}}\)

★ Perimetrul paralelogramului

Fie paralelogramul ABCD, cu AB paralelă cu CD și AD paralelă cu BC.

• perimetrul paralelogramului este egal cu suma lungimilor laturilor acestuia:



\({P_{ABCD}= AB + BC+CD+AD}\)

\({\textcolor{white}{P_{ABCD}}=2AB + 2AD }\)

\({\textcolor{white}{P_{ABCD}}=2(AB + AD) }\)

Exersează 1