Compararea puterilor cu aceeași bază sau cu același exponent
* * *
Atunci când vorbim de puterea unui număr natural, ne gândim imediat la o înmulțire repetată. De exemplu, 25 se citește „2 la puterea a cincea” sau „2 la a cincea” și înseamnă că pe 2 îl înmulțim cu el însuși de 5 ori. 2 se numește bază, iar 5 este exponent.

Am învățat ce înseamnă puterea unui unui natural, am învățat regulile de calcul cu puteri; acum vom învăța să comparăm puterile: care putere este mai mare, care putere este mai mică? Avem trei cazuri:
 comparăm puteri care au aceeași bază;
comparăm puteri care au aceeași bază;
 comparăm puteri care au același exponent;
comparăm puteri care au același exponent;
 comparăm puteri care au baze și exponenți diferiți (alt articol; am împărțit „Compararea puterilor” în două articole, pentru că un singur articol ar fi prea lung).
comparăm puteri care au baze și exponenți diferiți (alt articol; am împărțit „Compararea puterilor” în două articole, pentru că un singur articol ar fi prea lung).
Compararea puterilor cu aceeași bază
Să ordonăm crescător puterile: 20, 21, 22, 23, 24, 25, 26, 27.
Calculăm primele 8 puteri ale lui 2; 2 la puterea 0 este 1 (orice număr ridicat la puterea 0 este 1), 2 la puterea 1 este 2, 2 la puterea a doua este 2 înmulțit cu 2, adică 4; 2 la puterea a treia este egal cu 2 înmulțit cu el însuși de 3 ori. Pentru a lucra mai ușor, folosim regulile de calcul cu puteri: atunci când înmulțim două puteri cu aceeași bază, scriem baza și adunăm exponenții. Invers, putem scrie exponentul ca o sumă de doi sau mai mulți termeni, apoi scriem puterea respectivă ca produs de două sau mai multe puteri, cu exponenții egali cu termenii sumei. Astfel, pentru 2 la puterea a treia procedăm astfel: 3 este egal cu 2 plus 1, deci 2 la a treia este egal cu 2 la puterea a doua înmulțit cu 2 la puterea 1, adică este egal cu 2 la a doua înmulțit cu 2. Mai departe, 2 la puterea a patra este egal cu 2 la puterea a treia înmulțit cu 2, 2 la puterea a cincea este egal cu 2 la a patra înmulțit cu 2, 2 la a șasea este egal cu 2 la a cincea înmulțit cu 2, iar 2 la a șaptea este egal cu 2 la a șasea înmulțit cu 2.

Observăm că dintre două puteri cu aceeași bază, este mai mare cea cu exponentul mai mare. Putem să mai spunem că dintre două puteri cu aceeași bază, este mai mică cea cu exponentul mai mic.

Reținem regula pe care o vom aplica în cazul puterilor cu baze egale:

Exemplu
În grădina din fața casei, doi copii se joacă cu mașinuțele. 
Copiii șușotiră puțin între ei, apoi Alex zise:
- Îți spunem câte mașinuțe avem fiecare, bunicuțule. Eu am 3 la puterea a patra mașinuțe.
- Iar eu, 3 la puterea a treia, adăugă Ionuț.
- Spune mata, cine are mai multe mașinuțe? Fără să calculezi! (Am folosit mașinuțe desenate de OpenClipart-Vectors de la Pixabay)
Să-l ajutăm pe bunic: ce număr este mai mare, 34 sau 33? Cele două puteri au aceeași bază (baza 3). Exponenții sunt 4 și 3; cum 4 este mai mare decât 3, înseamnă că 34 este mai mare decât 33. Deci Alex are mai multe mașinuțe decât Ionuț.

Compararea puterilor cu același exponent
Să comparăm numerele 25 și 35. Observăm că cele două puteri au baze diferite (2 și 3), dar au același exponent, egal cu 5. Calculăm 25 și 35:

25 este mai mic decât 35; să comparăm primele puteri ale lui 2 cu primele puteri ale lui 3:
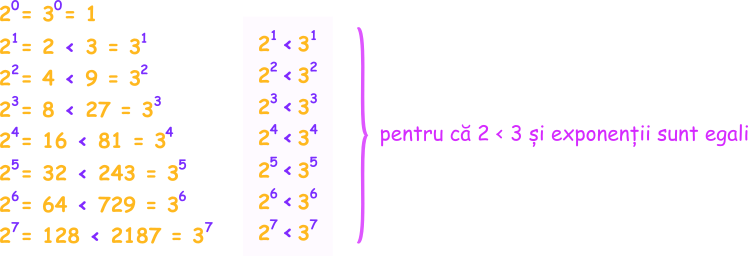
Observăm că dintre două puteri cu același exponent, este mai mare cea cu baza mai mare. Înseamnă că atunci când avem de comparat două puteri cu exponenți egali, comparăm bazele. Reținem regula:

Vrei să te verifici? Ai aici exerciții și probleme:
Puteți citi și ...
Compararea puterilor cu baze diferite și exponenți diferiți
Puterea cu exponent natural a unui număr natural
Împărțirea în grupe egale. Numărul elementelor dintr-o grupă
Legătura dintre împărțire și înmulțire
Împărțirea exactă (cu rest zero) a numerelor naturale

 Compararea puterilor cu aceeași bază
Compararea puterilor cu aceeași bază Încearcă și tu!
Încearcă și tu!


