Compararea puterilor cu baze diferite și exponenți diferiți
Atunci când este posibil, încercăm să rescriem puterile (folosind regulile de calcul cu puteri) astfel încât să comparăm două puteri cu aceeași bază sau cu același exponent.
Aducem puterile la aceeași bază
Exemple
 Să comparăm numerele 95 și 38. Observăm că bazele sunt diferite, la fel și exponenții. Înseamnă că nu putem aplica regulile pe care le-am stabilit mai sus. Cum facem?
Să comparăm numerele 95 și 38. Observăm că bazele sunt diferite, la fel și exponenții. Înseamnă că nu putem aplica regulile pe care le-am stabilit mai sus. Cum facem?
Avem de comparat numerele 95 și 38. Pe 9 îl putem scrie ca 32; înseamnă că 95 este egal cu 9 la puterea 2 înmulțit cu 5, adică 9 la puterea 10 (folosim regulile de calcul cu puteri: atunci când avem de ridicat o putere la o altă putere, scriem baza și înmulțim exponenții). Vom compara două puteri cu aceeași bază, 310 și 38 (am adus puterile la aceeași bază - baza 3). Fiind puteri cu aceeași bază, comparăm exponenții: 10 este mai mare decât 8, înseamnă că 310 este mai mare decât 38. Obținem că 95 este mai mare decât 38.

 Să comparăm numerele 57 și 253. Cele două numere au bazele diferite, la fel și exponenții. Cum le comparăm?
Să comparăm numerele 57 și 253. Cele două numere au bazele diferite, la fel și exponenții. Cum le comparăm?
Observăm că 25 este egal cu 52. Acesta este un indiciu important: înseamnă că putem aduce cele două numere la aceeași bază (baza 5). Dacă 25 este egal cu 52, atunci 253 este egal cu (52)3, adică 253 este egal cu 56 (ridicăm o putere la o altă putere - scriem baza și înmulțim exponenții).
Avem deci de comparat numerele 57 și 56, care au aceeași bază (baza 5). Comparăm exponenții: 7 este mai mare decât 6, deci 57 este mai mare decât 56.
Înseamnă că 57 este mai mare decât 253.

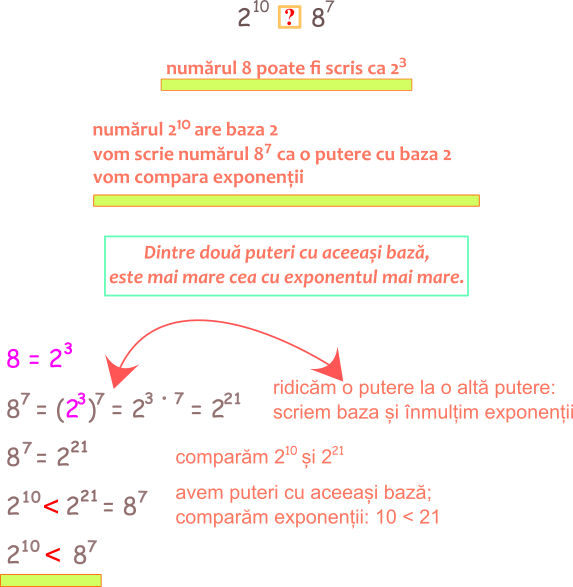
 Să comparăm numerele 210 și 87. Cele două numere au bazele diferite, la fel și exponenții.
Să comparăm numerele 210 și 87. Cele două numere au bazele diferite, la fel și exponenții.
 Observăm că 8 poate fi scris ca o putere cu baza 2: 8 este egal cu 23.
Observăm că 8 poate fi scris ca o putere cu baza 2: 8 este egal cu 23.
 Înseamnă că 87 este egal cu (23)7,
Înseamnă că 87 este egal cu (23)7,
 adică 87 este egal cu 221 (am ridicat o putere la altă putere, scriind baza și înmulțind exponenții).
adică 87 este egal cu 221 (am ridicat o putere la altă putere, scriind baza și înmulțind exponenții).
 Înseamnă că avem de comparat numerele 210 și 221, care au aceeași bază;
Înseamnă că avem de comparat numerele 210 și 221, care au aceeași bază;
 comparăm exponenții: 10 este mai mic decât 21, deci 210 este mai mic decât 221,
comparăm exponenții: 10 este mai mic decât 21, deci 210 este mai mic decât 221,
 adică 210 este mai mic decât 87.
adică 210 este mai mic decât 87.
Aducem puterile la același exponent
Exemple
 Să comparăm numerele 46 și 53. Observăm că bazele sunt diferite, la fel și exponenții. Cum comparăm numerele?
Să comparăm numerele 46 și 53. Observăm că bazele sunt diferite, la fel și exponenții. Cum comparăm numerele?
Exponentul primei puteri, 6, poate fi scris ca un produs cu unul dintre factori egal cu 3 (exponentul celei de-a doua puteri este 3), astfel: 2 înmulțit cu 3 sau 3 înmulțit cu 2 (înmulțirea este comutativă). Înseamnă că 46 este egal cu (42)3, adică 46 este egal cu 163.
Comparăm acum două puteri cu același exponent: 163 și 53. Comparăm bazele: 16 este mai mare decât 5, deci 163 este mai mare decât 53.

 Să comparăm numerele 330 și 420. Bazele sunt diferite, la fel și exponenții.
Să comparăm numerele 330 și 420. Bazele sunt diferite, la fel și exponenții.
Exponenții 30 și 20 pot fi scriși ca produse de factori astfel încât un factor este comun: 30 este egal cu 3 înmulțit cu 10, iar 20 este egal cu 2 înmulțit cu 10. Factorul comun este 10; vom rescrie cele două puteri astfel încât să avem puteri cu același exponent, egal cu 10.

Numerele 330 și 420 pot fi scrise ca puteri cu exponentul 2 sau 5 (exponenții 30 și 20 pot fi scriși ca produse care au comuni factorii 2 și 5). Indiferent de varianta pe care o alegem, rezultatul este același: 330 este mai mare decât 420.
 Să comparăm numerele 510 și 38. Bazele sunt diferite, la fel și exponenții.
Să comparăm numerele 510 și 38. Bazele sunt diferite, la fel și exponenții.
 Scriem exponenții ca produse, astfel încât să aibă un factor comun. Factorul comun va fi exponentul comun: 10 este egal cu 2 înmulțit cu 5.
Scriem exponenții ca produse, astfel încât să aibă un factor comun. Factorul comun va fi exponentul comun: 10 este egal cu 2 înmulțit cu 5.
 8 este egal cu 2 înmulțit cu 4.
8 este egal cu 2 înmulțit cu 4.
 Folosim regulile de calcul cu puteri pentru a scrie cele două numere ca puteri cu același exponent.
Folosim regulile de calcul cu puteri pentru a scrie cele două numere ca puteri cu același exponent.

Puteți citi și ...
Compararea puterilor cu aceeași bază sau cu același exponent
Puterea cu exponent natural a unui număr natural
Împărțirea în grupe egale. Numărul elementelor dintr-o grupă
Legătura dintre împărțire și înmulțire
Împărțirea exactă (cu rest zero) a numerelor naturale

 Aducem puterile la aceeași bază
Aducem puterile la aceeași bază Încearcă și tu!
Încearcă și tu!