Ce rezolvăm azi?
Pentru arhiva „Problema zilei”, click aici
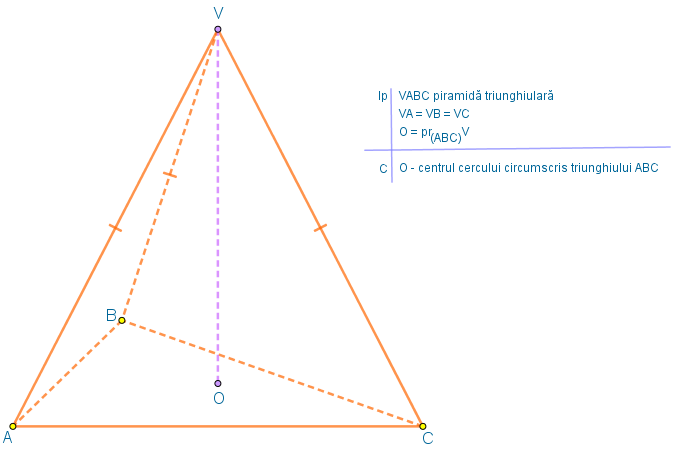
Fie VABC o piramidă triunghiulară astfel încât VA = VB = VC și punctul O este proiecția vârfului V pe planul triunghiului (ABC). Arătați că punctul O este centrul cercului circumscris triunghiului ABC.
Rezolvarea este mai jos pe pagină (click aici).
***
***
Rezolvare
Proiecția punctului V pe planul (ABC) este piciorul perpendicularei din punctul V pe planul (ABC). Adică VO este perpendicular pe planul (ABC) (înseamnă că VO este perpendicular pe orice dreaptă conținută în planul (ABC)).
Spunem că un cerc este circumscris unui triunghi dacă vârfurile triunghiului se află pe cercul respectiv; triunghiul este înscris în cercul respectiv. Centrul cercului circumscris unui triunghi se află la intersecția mediatoarelor laturilor acestuia (mediatoarea unui segment este perpendiculara dusă prin mijlocul acelui segment). Înseamnă că segmentele care unesc centrul cercului circumscris triunghiului și vârfurile acestuia sunt raze ale cercului, deci sunt congruente (egale).

Arătăm că segmentele AO, BO și CO sunt congruente; înseamnă că ele sunt razele cercului circumscris triunghiului ABC, deci punctul O este centrul acestui cerc.
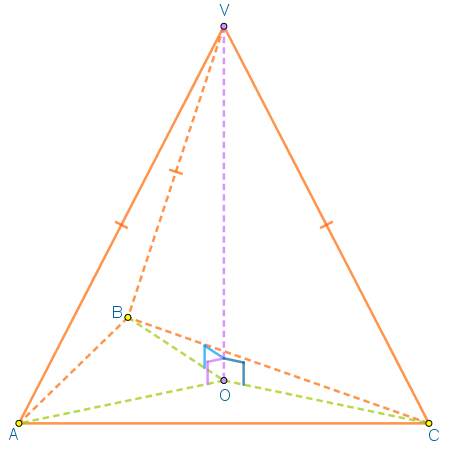
O metodă prin care putem să arătăm că două segmente sunt congruente este să le încadrăm în două triunghiuri congruente. Încadrăm segmentele AO, BO și CO în triunghiurile VOA, VOB și VOC și arătăm că aceste triunghiuri sunt congruente.
VO este perpendicular pe planul triunghiului (ABC), deci este perpendicular pe AO, BO și CO. Înseamnă că triunghiurile VOA, VOB și VOC sunt dreptunghice în O. Ele au o catetă comună (cateta VO) și ipotenuzele congruente (muchiile piramidei sunt ipotenuze în triunghiurile dreptunghice VOA, VOB și VOC și sunt congruente - știm din ipoteză). Înseamnă că cele trei triunghiuri sunt congruente (cazul ipotenuză-catetă). Rezultă că AO, BO și CO sunt congruente.

